v2306: New and improved numerics
The gradient caching mechanism (originally available for the finite-volume framework) has been applied to the finite-area framework.
When enabled, gradient fields are calculated only when dependent fields change, and stored in memory on the mesh database for later re-use, saving additional costly re-evaluations.
An example usage in system/faSolution file is as follows:
cache
{
grad(h);
grad(Us);
}
Source code
Merge request
The new preconditioners distributedDILU, distributedDIC add Red-Black type parallel behaviour variants to the DILU, DIC preconditioners. These new preconditioners are especially useful for solving the coarsest level of the GAMG solver:
p
{
solver GAMG;
// Explicit specify solver for coarse-level correction to override
// preconditioner
coarsestLevelCorr
{
solver PCG;
preconditioner distributedDIC;
}
}
On very large core counts the scaling bottleneck can become the global reductions in the coarsest level solution and this is where the distributed preconditioners can lower the amount of sweeps and hence reductions (at the cost of additional halo-swaps). For a large case on 4096 cores:
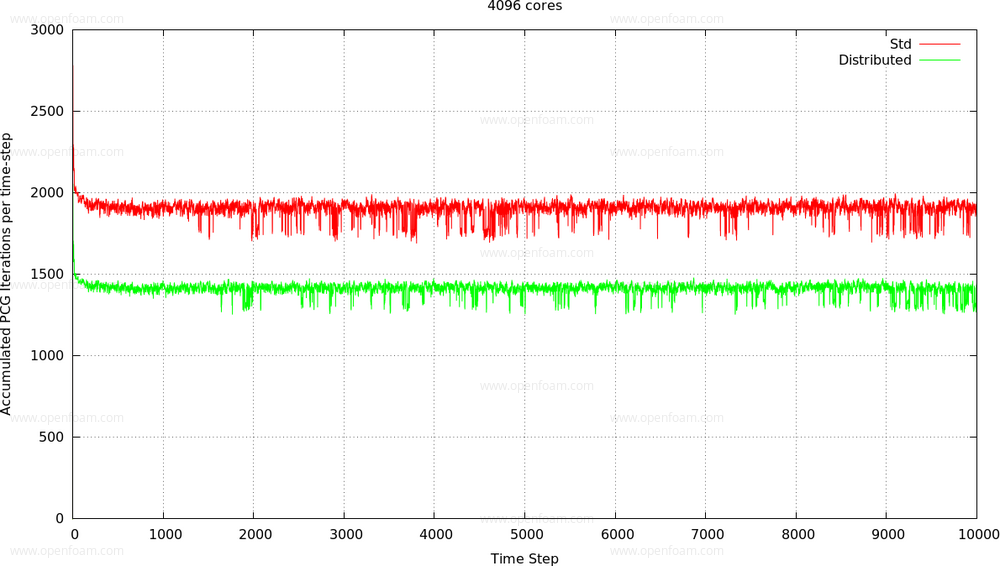
This performance benefit is demonstrated in the timings:
| preconditioner | Execution time |
|---|---|
| DIC | 8687s |
| distributedDIC | 6326s |
Note that using the distributed preconditioners generally only make sense if the computation is global-reduction bound. Compared to the non-distributed variants they will lower the number CG sweeps (and hence reductions) at the cost of additional halo-sweeps. On smaller numbers of cores this might not be beneficial. Similar if the number of CG sweeps is low anyway, e.g. when solving to a relative tolerance.
The same strategy can be applied to other coupled boundary conditions, e.g. cyclic, cyclicAMI. In the forward loop the effect of 'neighbour' on 'owner' patch is included, in the backwards loop the opposite. This is switched with the coupled switch (default is on):
solver PCG;
preconditioner distributedDIC;
coupled false; // do not precondition across non-processor coupled
In the case of cyclicAMI there is a limitation that the two sides should be exclusively on different processors, or not be distributed at all.
Since the new preconditioners are quite expensive to construct they are cached inside the linear solvers. This only affects the coarsest-level correction solver inside the GAMG.
Source code
- $FOAM_SRC/meshTools/matrices/lduMatrix/preconditioners/distributedDILUPreconditioner/distributedDILUPreconditioner.H
- $FOAM_SRC/meshTools/matrices/lduMatrix/preconditioners/distributedDILUPreconditioner/distributedDICPreconditioner.H
References
Merge request
A new drop-in replacement for the PCG linear solver, FPCG, reduces the number of reductions per sweep from three to two. This should yield improved parallel scaling, particularly for larger core counts where parallel reductions may lead to bottlenecks, especially when solving the coarsest level in the GAMG linear solver.
This solver offers a trade-off between the number of reductions and the additional storage/amount of pipelining. This can be compared to the PPCG solver which overlaps halo-swaps with reductions (but needs additional storage).
Note that FPCG requires one extra preconditioning step and therefore may be less beneficial for more complex preconditioners, e.g. GAMG
Attribution
- OpenCFD would like to acknowledge and thank Alon Zameret of Toga Networks for providing the code and elaborate discussions.
Source code
Merge request
Tensor inversion is required for, e.g. least squares calculation, and can be particularly troublesome when the tensor values are in-plane, e.g. essentially 2D. These are now handled by a "safe" inversion approach that adds robustness without the costly overhead of a pseudo inverse. This change primarily affects the robustness of some finite-area schemes.
Information of the cell-to-point and/or the point-to-cell addressing is required for different algorithms. Since this type of addressing can be relatively costly to calculate, it is cached whenever possible and reused to derive the missing addressing.
Although this is usually associated with a one-time cost, it can become a larger factor for meshes with topology changes which invalidate the cached values. The updated approach for rebuilding the addressing improves the speed by a factor of 1.4 to 2.4 times.
Attribution
- OpenCFD would like to acknowledge and thank Toga Networks for providing the code and elaborate discussions.
- issue 2715
- MR!596

