v2206: New and improved numerics
A new adjoint to the k-ω SST turbulence model is now available, to complement the existing adjoint to the Spalart-Allmaras model.
Making the "frozen turbulence" assumption, i.e. assuming that the turbulent viscosity field does not change when the shape changes throughout the optimisation, can lead to erroneously computed sensitivity derivatives. As an example, the drag sensitivity maps computed on the surface of the Ahmed body using the "frozen turbulence" assumption and the fully differentiated k-ω SST model are depicted below, featuring areas where the sign of the sensitivity map changes when turbulence is not differentiated.
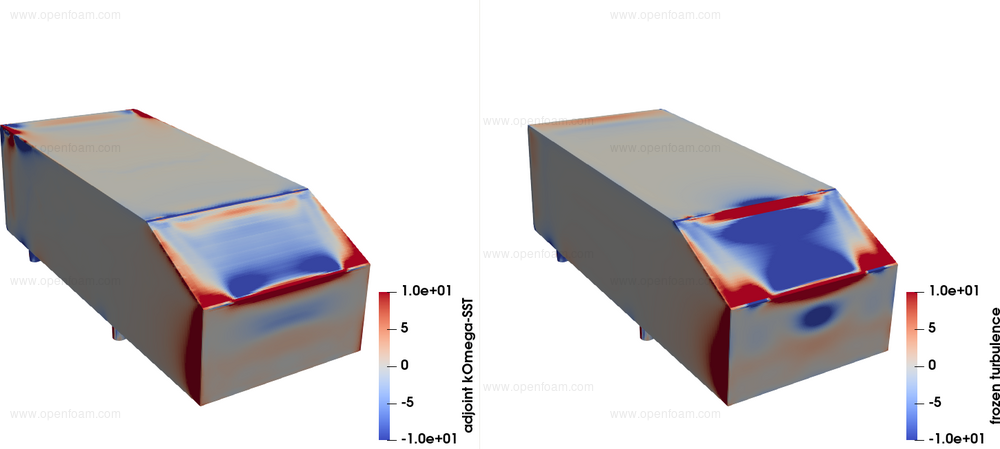
Taking this a step further and executing optimisations with "frozen turbulence" (FT) and "differentiated turbulence" (DT) highlights the need for differentiating the k-ω SST model in this case.
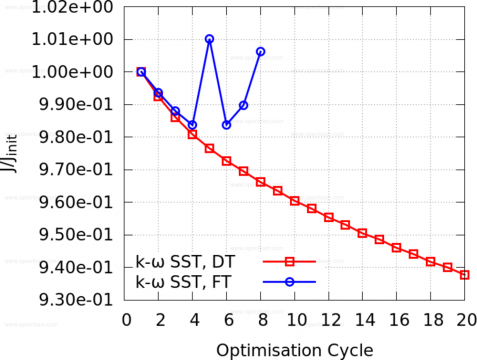
The DT approach reduces drag by more the 6% within 20 optimisation cycles whereas the optimisation based on the FT assumption diverges after the fourth cycle.
A further comparison is shown below that compares the sensitivity maps from the new k-ω SST model (top) and Spalart-Allmaras model (bottom):
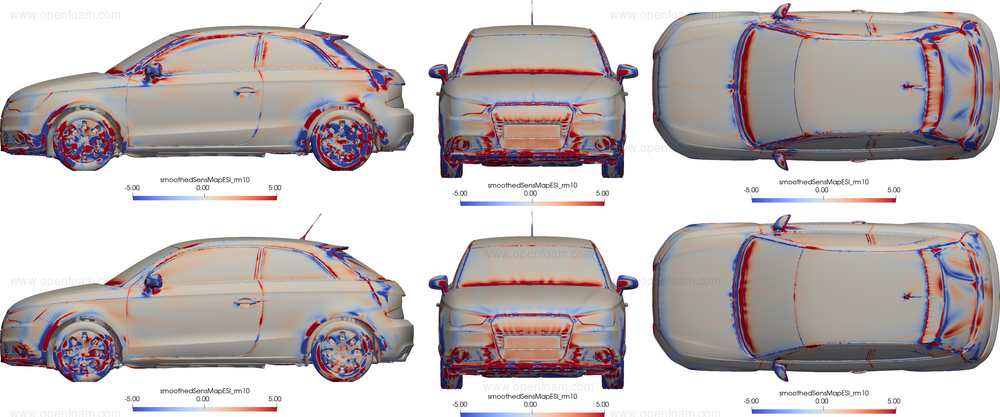
The work is based on the work of Kavvadias et al. with changes in the discretisation of a number of differential operators and the formulation of the adjoint to the wall functions employed by the primal model.
Source code
Tutorials
- $FOAM_TUTORIALS/incompressible/adjointOptimisationFoam/shapeOptimisation/naca0012/kOmegaSST/lift
- $FOAM_TUTORIALS/incompressible/adjointOptimisationFoam/shapeOptimisation/sbend/turbulent/kOmegaSST/opt
References
- Kavvadias, I., Papoutsis-Kiachagias, E., Dimitrakopoulos, G., & Giannakoglou, K. (2014). The continuous adjoint approach to the k–$omega$ SST turbulence model with applications in shape optimization. Engineering Optimization, 47(11), 1523-1542. https://doi.org/10.1080/0305215X.2014.979816
Attribution
- The initial implementation, as described in the reference, was performed by Dr. Ioannis Kavvadias during his PhD at PCOpt/NTUA.
- The current version of the code was revamped by PCOpt/NTUA and FOSS GP and was integrated in collaboration with OpenCFD.
The adjoint optimisation library has been updated, addressing three main aspects:
- Restarting a (partially) already ran optimisation is now easier and more accurate
- Adjoint solvers write/read their sensitivity derivatives under the uniform folder, to avoid potential loss of accuracy due to I/O.
- Volumetric B-Splines control points of each optimisation cycle are written under uniform and now additionally support binary I/O. As a consequence, the controlPointsDefinition in constant/dynamicMeshDict no longer needs to be changed to fromFile to perform the continuation, removing a potential source of miss-setups.
- The adjoint grid displacement field (ma) is now appended by the name of the adjoint solver, if more than one exists. This facilitates continuation since, before the change, only the ma field of the last adjoint solver was written to file. No changes to fvSchemes or fvSolution are necessary.
- Reduced turnaround times
- A number of changes to reduce the solution turnaround time of the adjoint equations (see bac1d8ba for details). In brief, these include caching of some expensive but constant quantities and removing some coding shortcomings. All cases should see some benefit, e.g. around 9.5% reduction in the turnaround time of the adjoint solver for the motorbike tutorial, but the latter can be even more pronounced in cases with many outlet boundaries.
- Reduced peak memory consumption
-
The peak memory consumption of the adjoint code is observed during the computation of sensitivity derivatives, when using either the FI or the E-SI approach, due to the need of manipulating a number of volTensorFields necessary to compute the multiplier of the spatial gradient of the grid sensitivities. This part of the code has been re-written to reduce this peak memory consumption.
-
Attribution
- The adjoint library was updated/reviewed by PCOpt/NTUA, FOSS GP and OpenCFD
Source code
The QR decomposition algorithm has been refactored, simplified and improved, by utilising algorithms from the open-source public-domain Template Numerical Toolkit (TNT).
The improved QRMatrix solver performs QR decomposition on a given scalar/complex rectangular/square matrix A as follows:
A = Q R
or in case of a QR decomposition with column pivoting:
A P = Q R
where
- Q : Unitary/orthogonal matrix
- R : Upper triangular matrix
- P : Permutation matrix
The QR decomposition algorithm can compute the full-size and economy-size QR decompositions with and without column pivoting. The output types can be selected as either Q-matrix or R-matrix or both.
Source code
Tutorial
Merge request
References
- Pozo, R. (1997). Template Numerical Toolkit for linear algebra: High performance programming with C++ and the Standard Template Library. The International Journal of Supercomputer Applications and High Performance Computing, 11(3), 251-263. DOI:10.1177/109434209701100307
The SemiImplicitSource now supports a new exprField specification, which allows flexibility when defining the location or intensity of sources, e.g.:
{
type scalarSemiImplicitSource;
volumeMode specific;
selectionMode all;
sources
{
tracer0
{
explicit
{
type exprField;
functions
{
square
{
type square;
scale 0.0025;
level 0.0025;
frequency 10;
}
}
expression
#{
(hypot(pos().x() + 0.025, pos().y()) < 0.01)
? fn:square(time())
: 0
#};
}
}
}
}
Note that the SemiImplicitSource uses a new sources dictionary entry with explicit and/or implicit contributions in an effort to make the input entries more intuitive than the older injectionRateSuSp syntax.
Tutorials
Source code

