OpenFOAM® v1906: New and improved numerics

New adjoint optimisation

OpenFOAM v1906 includes the first release of a major new set of functionality targeting automated gradient-based optimisation loops assisted by the continuous adjoint method. The code is under active development and further extensions will be released in future official OpenFOAM releases.

This is the first project sponsored and released under OpenFOAM’s new Governance framework.

Adjoint methods are used to compute the gradient (or sensitivity derivative) of engineering quantities, usually referred to as objective functions, e.g. drag, lift, with respect to a number of so-called design variables, e.g. control points parameterizing an aerodynamic shape. The major advantage of adjoint methods is that the cost of computing this gradient is, practically, independent of the number of design variables. To achieve this, a single set of adjoint PDEs is solved to compute the gradient of an objective function. This reduced cost allows for computing the so-called sensitivity maps, i.e. the gradient of an objective function with respect to the normal displacement of boundary nodes, with thousands or millions of design variables as shown below. Sensitivity maps are a valuable tool that can guide the designer in early design stages and pin-point the areas with the greatest optimisation potential.

OpenFOAM v1906 includes the adjoint to incompressible steady-state flows, supporting also the differentiation of the Spalart-Allmaras model, with and without wall functions. The available objective functions include forces and moments for external aerodynamics and total pressure losses for internal aerodynamics. Sensitivities are computed with respect to the normal displacement of the boundary wall nodes/faces.

The main executable solving the flow and adjoint equations and computing sensitivity derivatives is adjointOptimisationFoam, supporting also multi-point computations, i.e. solving the flow and adjoint equations and computing sensitivities in a number of operating conditions.

Most of the parameters pertaining to adjointOptimisationFoam are set-up through a the input optimisationDict dictionary, located in the system directory. As new PDEs are solved, additional entries are required in the fvSolution and fvSchemes dictionaries; boundary conditions for the adjoint fields also need to be prescribed in the start time directory.

Source code

$FOAM_SOLVERS/incompressible/adjointOptimisationFoam
$FOAM_SRC/optimisation/adjointOptimisation/adjoint

Examples

$FOAM_TUTORIALS/incompressible/adjointOptimisationFoam

Attribution

The software was developed by PCOpt/NTUA and FOSS GP with contributions from

• Dr Evangelos Papoutsis-Kiachagias,
• Konstantinos Gkaragounis,
• Professor Kyriakos Giannakoglou,
• Dr Andrew Heather

and contributions in earlier version from

• Dr Ioannis Kavvadias,
• Dr Alexandros Zymaris,
• Dr Dimitrios Papadimitriou

References

• A.S. Zymaris, D.I. Papadimitriou, K.C. Giannakoglou, and C. Othmer. Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows. Computers & Fluids, 38(8):15281538, 2009.
• E.M. Papoutsis-Kiachagias and K.C. Giannakoglou. Continuous adjoint methods for turbulent flows, applied to shape and topology optimization: Industrial applications. 23(2):255299, 2016.
• I.S. Kavvadias, E.M. Papoutsis-Kiachagias, and K.C. Giannakoglou. On the proper treatment of grid sensitivities in continuous adjoint methods for shape optimization. Journal of Computational Physics, 301:118, 2015.

Integration

The code has been integrated jointly by OpenCFD and NTUA

User guide

A PDF guide prepared by NTUA is available here

Improved restart behaviour

This release includes improvements to enable smooth restart behaviour. Testing has shown bit-perfect restart on low to medium complexity incompressible cases.

The cumulative continuity error is now written/read from the file <time>/uniform/cumulativeContErr to ensure that the printed continuity error is correctly restored.

Turbulence models have been assessed and updated as necessary. The nutUSpaldingWallFunction boundary condition performs an iterative procedure to obtain the friction velocity 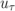, exiting when the error reduces to within a specified tolerance. This can now be specified and on restart will preserve the initial nut values if they are sufficiently converged:

Note that this tolerance should be tight to avoid triggering this special behaviour during running.

Source code

$FOAM_SRC/finiteVolume/cfdTools/general/include/initContinuityErrs.H
$FOAM_SRC/TurbulenceModels/turbulenceModels/lnInclude/nutUSpaldingWallFunctionFvPatchScalarField.H

New wall distance method

Some turbulence models require the distance to the nearest wall patch. The set of methods to calculate this distance has been extended to include an exact method. This triangulates the wall geometry and returns the correct nearest point on the nearest triangle of the nearest wall face, independent of the decomposition.

The new method is made available by adding library libdistributed.so to the controlDict set-up, e.g.

Select in system/fvSchemes the correct wallDist scheme:

The resulting distance can be tested with the test application Test-wallDist in applications/test/wallDist. For example, the following image shows the distance field for a modified cavity tutorial case where only the top patch is of type wall.

Note: the exact distance method is complex compared to other variants, reflected in the time taken to compute the distance field, e.g. on a large case:

• meshWave : 33 s
• exact : 859 s

Source code

$FOAM_SRC/lagrangian/intermediate/submodels/HeterogeneousReactingModel

Solver

$FOAM_SOLVERS/lagrangian/reactingParcelFoam/reactingHeterogenousParcelFoam

Tutorial

$FOAM_TUTORIALS/lagrangian/reactingHeterogenousParcelFoam/rectangularDuct

Improved GAMG solver controls

The GAMG framework employs a linear solver to solve the residual correction on the coarsest level. This is currently:

• a direct solver if directSolveCoarsest has been selected
• an iterative CG solver, e.g. DICPCG for symmetric matrices, or DILUPBiCGStab for asymmetric matrices. In this release the iterative coarse-level solver controls are user-selectable.

Each solver dictionary using GAMG can now optionally provide a sub-dictionary coarsestLevelCorr containing the settings for the coarsest level solver. Tolerances are taken from the parent-level GAMG entries if not specified.

The example above selects the PCG solver and a loose relative tolerance of 0.05. The absolute tolerance is taken from the GAMG settings.

In general it pays to use the best available solver at the coarse level since it contains so few cells, defined by the nCellsInCoarsestLevel entry, having a default value of 10. For parallel runs the communication overhead inside the coarse-level solver can be a performance bottleneck. Here it is advantageous to lower the number of coarse-level sweeps even if it slightly increases the overall number of GAMG cycles. The two useful controls are

• relTol : override the relative tolerance.
• maxIter : override the maximum number of iterations.

As a test the $FOAM_TUTORIALS/pisoFoam/LES/motorBike/motorBikeLES tutorial was run for 10 iterations. Employing a loose relative tolerance for the coarse level solver shows a drastic reduction in the number of sweeps of the PCG solver, whereas the number of GAMG cycles remains almost constant:

Coarse-level solver performance can be observed by setting the following debug switches in system/controlDict:

The output will now include the residuals of the coarse-level solver, e.g.

Tutorial

$FOAM_TUTORIALS/pisoFoam/LES/motorBike/motorBikeLES

New mixed precision

OpenFOAM can be compiled to run with double-precision scalars (default) or single-precision scalars. In general only simple cases can be run in single-precision - for more complex cases the linear solvers will often not converge.

This release includes a new option to compile the linear solvers using double precision and the remaining code using single precision. The new mode is SPDP and can be selected with the command

Similarly, wmDP for double precision and wmSP for single precision. This will set the:

• environment variable WM_PRECISION_OPTION=SPDP and
• compilation flag WM_SPDP

The OpenFOAM header Arch field now shows the type of floating point used in the linear solvers by the solveScalar keyword:

The main gain from running in single precision is in the memory used; a single precision build uses about 40% less memory than double precision. This also directly influences the performance for a bandwidth-limited code like OpenFOAM. In mixed precision there is about 30% less memory usage and 20% improved performance compared to double precision. Internal tests have indicated that the new setting is robust across a range of large external aero cases with little difference in statistics.

Mixed precision only affects the linear solver; it will not help if the problem area is outside the linear solver, e.g. the following are unlikely run in mixed precision:

• snappyHexMesh
• cyclicAMI
• combustion
• Lagrangian

Note that fields in mixed precision are written in single precision since only the linear solver operates in double precision. Transfer from single-to-double precision and double-to-single is only supported in ASCII format.

The wm macros are convenient in mixed workflows:

Compile both versions:

Run set-up in double precision, run simulation mixed:

Overset improvements

There are two main improvements to the overset framework:

• a faster version of the inverse-distance weighted stencil: trackingInverseDistance; and
• remote contributions are handled more consistently

trackingInverseDistance

The new oversetInterpolation method employs a voxel mesh to accelerate geometric queries. It requires the regions of interest, defined using a single bounding box, and its number of subdivisions in the x, y and z directions (per mesh):

This method is still under active development, where testing has shown a large improvement in the mesh update time.

Parallel interpolation

The main building block in the overset method is interpolation from cell(s) to cell. For moving meshes there is no guarantee that the donor cells reside on the same processor as the interpolated cell (acceptor cell). In previous versions remote-cell contributions provided consistent effects in the vector-matrix multiplication (the building block of most linear solvers) but not in other routines. In this version remote-cell contributions are handled in exactly the same way as ’normal’ processor boundaries, by dynamically constructing processor boundaries, leading to parallel consistent linear solver behaviour:

• the initial residual for a constant field will now be 1
• consequently the solver behaviour will be more consistent with non-parallel runs
• future interfacing of external solvers will not need any special handling of overset provided that processor boundaries are handled

Example of v1812:

Same case v1906: The initial residual for Ux now includes remote contributions and so does normalise to 1. This will also affect the scaling of the residual. Note that there are some small differences in the treatment of the pressure leading to a slight difference in residuals.