Overview
Flow physics:
- Internal flow
- Moderate Reynolds number
- Spanwise direction: Statistically homogeneous
- Streamwise and channel-height directions: Statistically developing
- Newtonian, single-phase, incompressible, non-reacting
Solver:
Tutorial case:
Keywords: Detached eddy simulation (DES), Large eddy simulation (LES), Synthetic turbulence generation Smagorinsky sub-filter scale model, pimpleFoam, pisoFoam
Physics and Numerics
Physical domain:
- The case is a statistically-developing internal flow through parallel smooth walls which are two characteristic-length apart.
- \( x \): Longitudinal direction (Mean-flow direction)
- \( y \): Vertical direction (Wall-normal direction)
- \( z \): Spanwise direction (Statistically homogeneous direction)
- \( O \): Origin at the left-bottom corner of the numerical domain
Physical modelling:
- Reynolds number based on friction velocity: \( \text{Re}_{u_\tau} = |\mathbf{U}_\tau| \delta / \nu_\text{fluid} = 395\) [-]
- (Estimated) Friction velocity: \( \mathbf{U}_\tau = (1.0, 0.0, 0.0)\), and \( | \mathbf{U}_\tau | = u_\tau = 1.0 \) [m⋅s-1]
- Characteristic length (Channel half-height): \(\delta = 1.0 \) [m]
- Kinematic viscosity of fluid: \( \nu_{\text{fluid}} \approx 0.002532 \) [m2⋅s-1]
- Bulk velocity of flow: \( \mathbf{U}_b = (17.55, 0.00, 0.00)\) [m⋅s-1]
- Turbulence model: Large eddy simulation with the Smagorinsky sub-filter scale model utilising the van Driest wall-damping function. The sub-filter scale model constants:
- \( C_k \approx 0.02655\)
- \( C_e = 1.048 \)
- \( C_s \approx 0.065 \) -> \( C_s = (C_k \{C_k/C_e\}^{0.5} )^{0.5}\)
Numerical domain modelling:
- Shape: Rectangular prism
- Dimensions: \( (x, y, z) = (20.0\pi, 2.0, \pi)\) [m]
- Sketch:

Numerical domain (not in scale)
Spatial domain discretisation:
- Mesh type: Rectangular cuboid mesh
- Mesher: blockMesh
- Number of nodes, \(N\): \( (N_x, N_y, N_z) = (500, 46, 82)\) [nodes]
- Spatial resolution \((\Delta)\) distribution:
- Uniform in \((x, z)\)-directions
- Stretched in \((y)\)-direction; clustered nearby walls
- Uniform mesh particulars:
- \( \Delta_x^+ = (\Delta_x u_\tau )/\nu_{\text{fluid}} \approx 49.6\) [-]
- \( \Delta_z^+ \approx 15.1\) [-]
- Wall-normal mesh particulars:
- Simple grading expansion ratio: 25.0 -
- First wall-normal node height: \(\Delta_y^+ \approx 1.1\)
- Mesh details:

Mesh (Front part)
|

Mesh
|
Temporal domain discretisation:
- Time-step size: \( \Delta_t = 0.004\) [s]
- (Estimated) Courant-Friedrichs-Lewy (CFL) number based on \( \{ \overline{u_x} \}_{y^+ = 392} = 20.133\)[m⋅s-1]: CFL \(\approx 0.64\)
Equation discretisation:
Spatial derivatives and variables:
Temporal derivatives and variables:
Numerical boundary conditions:
- Velocity, \( \mathbf{U} \)
- Turbulent kinematic viscosity,
nut (i.e. \( \nu_t \))
| Patch | Condition | Value [m2⋅s-1] |
| Inlet | calculated | - |
| Outlet | calculated | - |
| Sides ( \(z\)-dir) | cyclic | - |
| Walls ( \(y\)-dir) | zeroGradient | - |
Solution algorithms and solvers:
- Pressure-velocity: PISO algorithm
- Parallel decomposition of spatial domain and fields: scotch
- The bandwidth of the coefficient matrix is minimised by renumberMesh
- Linear solvers:
Initialisation and sampling:
- Computation time for a single domain pass-through based on \( \{ \overline{U_x} \}_{y^+ = 392} = 20.133\)) [m2⋅s-1] \(\approx 3.121\) [s]
- Initialisation pass-throughs = \( \approx 2.7 \) [60]
- Sampling pass-throughs = \( \approx 24.5 \) [60]
Results
List of metrics:
- Prescribed vs. reproduced Reynolds stress tensor components at inlet patch
- \( \overline{u^\prime u^\prime} \) downstream development vs. \( x/ \delta \)
- \( \overline{v^\prime v^\prime} \) downstream development vs. \( x/ \delta \)
- \( \overline{u^\prime v^\prime} \) downstream development vs. \( x/ \delta \)
- Surface skin friction coefficient \(\mathrm{C}_f\) vs. \(x/ \delta \)
- Streamwise mean flow speed and Reynolds stress tensor components at uniform-interval downstream profiles
- Streamwise vorticity \( \omega_x \) at \(x/ \delta = 0.1\)
- Streamwise vorticity \( \omega_x \) at \(x/ \delta = 1.0\)
- Metrics are time and spanwise averaged
- \( \{ < \cdot > \} \) is the time-averaging operator
|
|
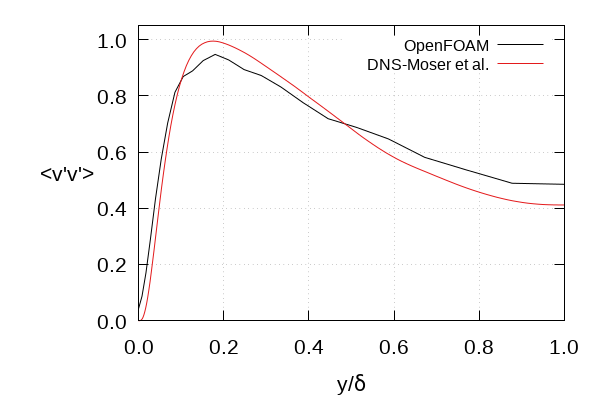
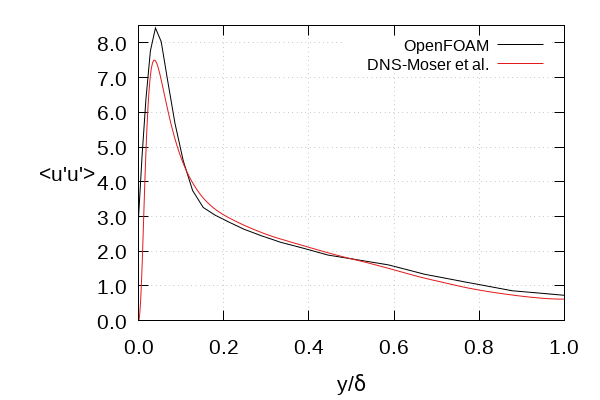
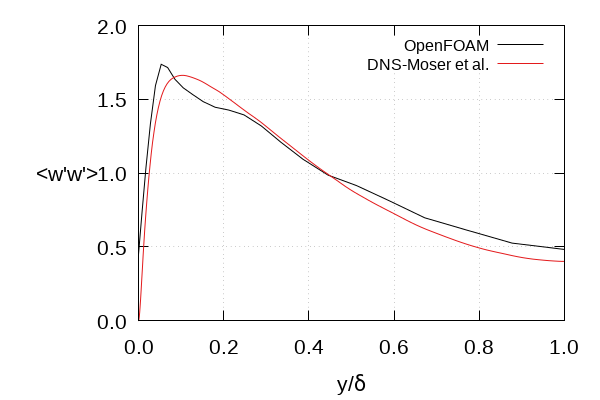
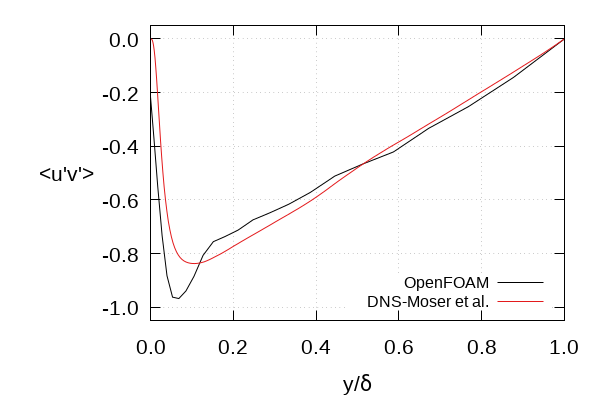
Prescribed vs. reproduced Reynolds stress tensor at inlet patch (Poletto et al., Fig. 4)
|
|
|
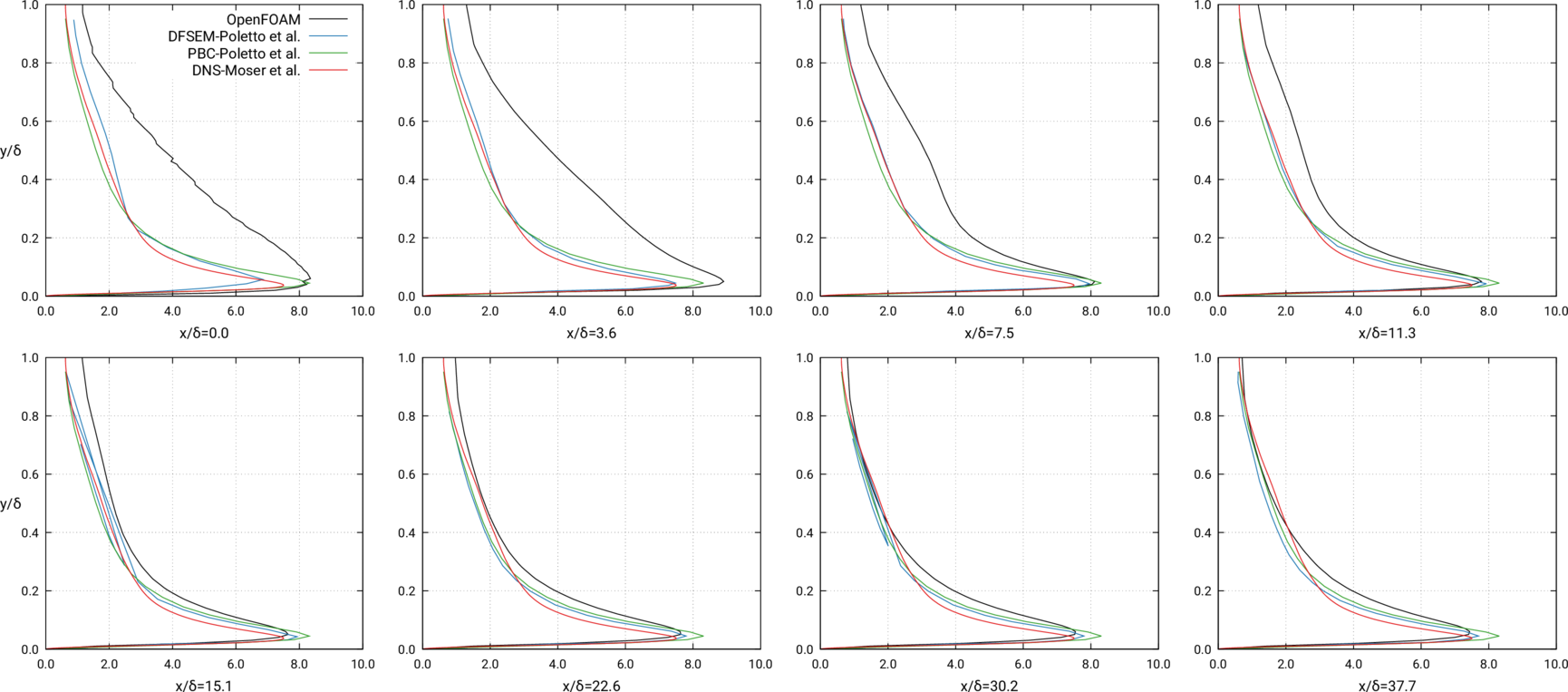
<u'u'>-component of Reynolds stress tensor - Downstream development (Poletto et al., Fig. 14)
|

<v'v'>-component of Reynolds stress tensor - Downstream development (Poletto et al., Fig. 15)
|
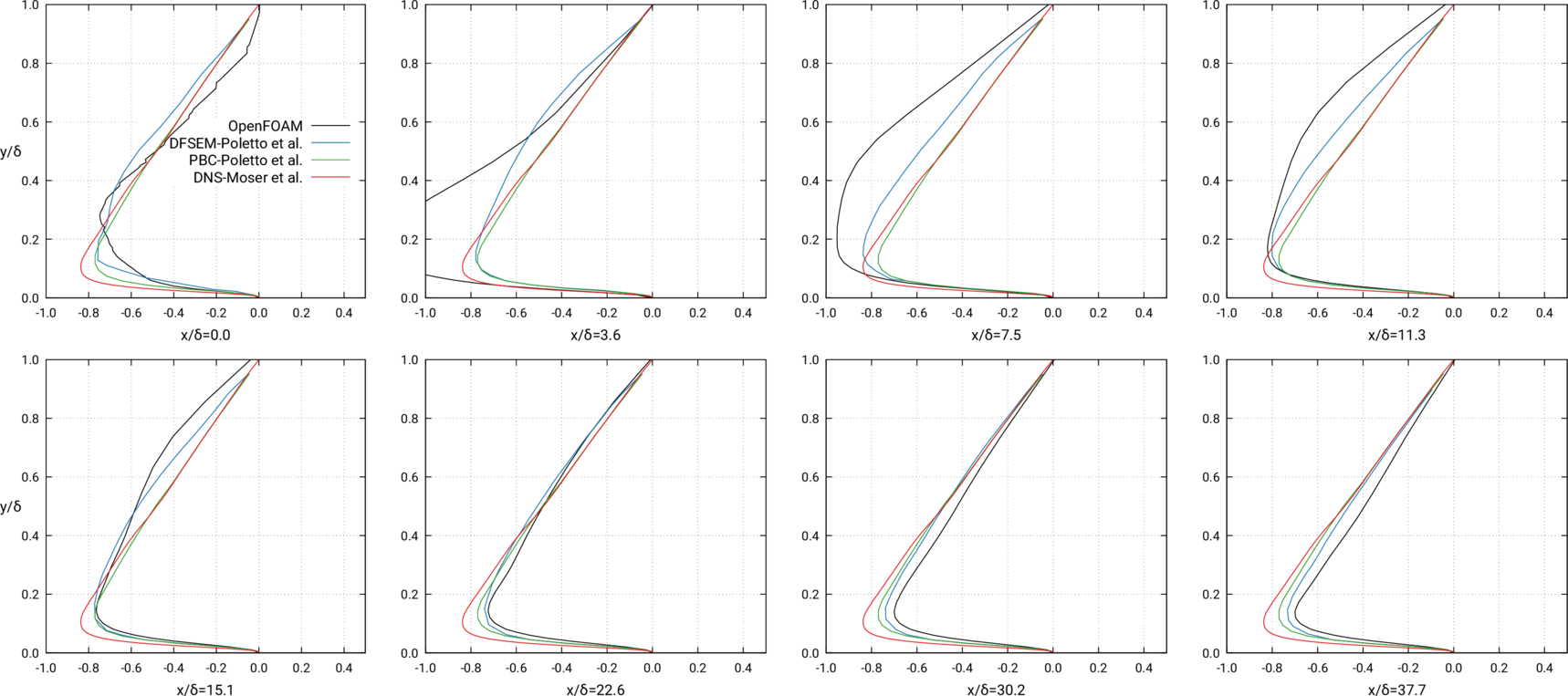
<u'v'>-component of Reynolds stress tensor - Downstream development (Poletto et al., Fig. 13)
|

Longitudinal skin friction coefficient at top patch - Downstream development (Poletto et al., Fig. 9)
|
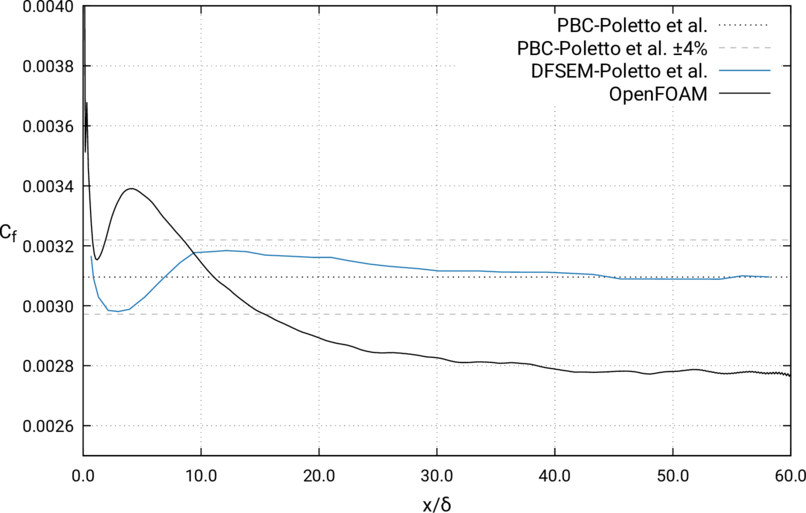
Longitudinal skin friction coefficient at bottom patch - Downstream development (Poletto et al., Fig. 9)
|

Streamwise vorticity component at y/δ=0.05 (Poletto et al., Fig. 11)
|

Streamwise vorticity component at y/δ=1.0 (Poletto et al., Fig. 12)
|
Resources
Note: Links will take you to the University of Texas at Austin website
Datasets for verifications (plain text)
Reynolds stress tensor profiles:
Mean velocity profiles:
Two-point velocity correlations (i.e. Auto- and cross-correlation functions):