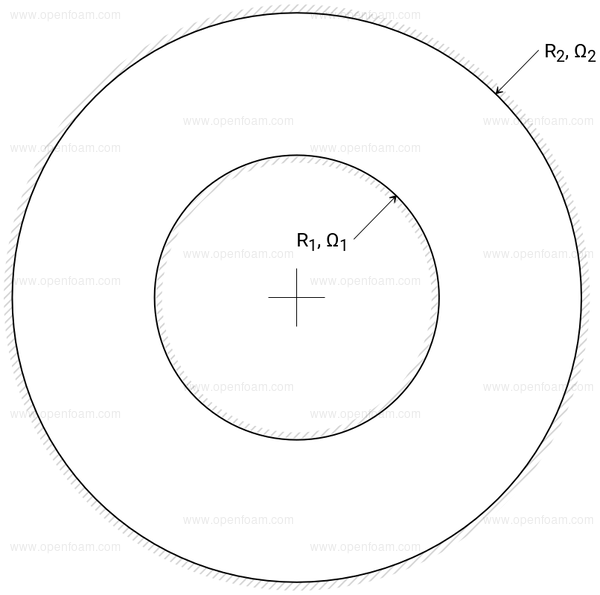
The case comprises two cylinders, with inner radius \( R_1 \) rotating with angular velocity \( \Omega_1 \), and outer radius \( R_2 \) rotating with angular velocity \( \Omega_2 \).
The laminar case corresponds to a Reynolds number of 100. where the Reynolds number os defined as:
\[ Re = \frac{|\u|_0 d}{\nu} \]
Where \( |\u|_0 \) is the angular velocity of the inner cylinder, i.e.
\[ |\u|_0 = \Omega_1 R_1 \]
and \( d \) is the distance between the cylinders, i.e. \( R_2 - R_1 \). Using an inner and outer radii of 1 and 2, respectively, and setting the kinematic viscosity to \( 1 \), the angular velocity of the inner cylinder is 100 rad/s.
Taylor [taylor_stability_1922] shows that the velocity, \(\u_{\theta} \) is described by:
\[ \u_{\theta} = A r + \frac{B}{r} \]
where \( A \) and \( B \) are constants defined as:
\[ A = \frac{\Omega_1 \left( 1 - \mu \frac{R_2^2}{R_1^2} \right)}{1 - \frac{R_2^2}{R_1^2}} \]
\[ B = \frac{R_1^2 \Omega_1 (1 - \mu)}{1 - \frac{R_1^2}{R_2^2}} \]
Here, \( \Omega_1 \) and \( \Omega_2 \) are the rotational speeds of the inner and outer cylinders, and
\[ \mu = \frac{\Omega_2}{\Omega_1} \]
The steady flow equations for this case, in cylindrical co-ordinates reduces to
\[ \frac{1}{\rho}\frac{\partial p}{\partial r} - \frac{\u_{\theta}^2}{r} = 0 \]
On integrating with respect to radius an expression for the pressure is recovered:
\[ p = \frac{A^2 r^2}{2} + 2 A B \ln (r) + \frac{B^2}{2 r^2} + C \]
The rotational velocity, \( \u_\theta \) can be directly reported during the calculation using a fieldCoordinateSystemTransform function object.
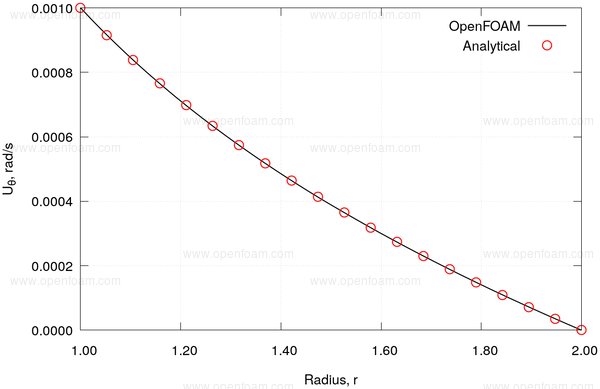
Rotational velocity as a function of radius | 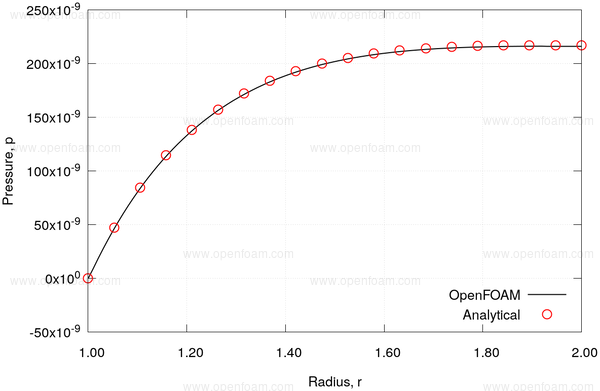
Pressure as a function of radius |
| Would you like to suggest an improvement to this page? | Create an issue |
Copyright © 2019 OpenCFD Ltd.