Flow physics:
Solver:
Tutorial case:
Keywords: Reynolds-averaged Navier-Stokes, simpleFoam
Physical domain:
Physical modelling:
Numerical domain modelling:
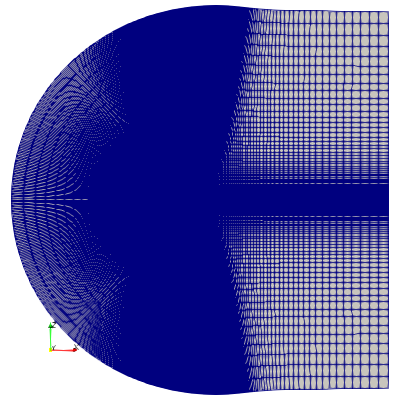
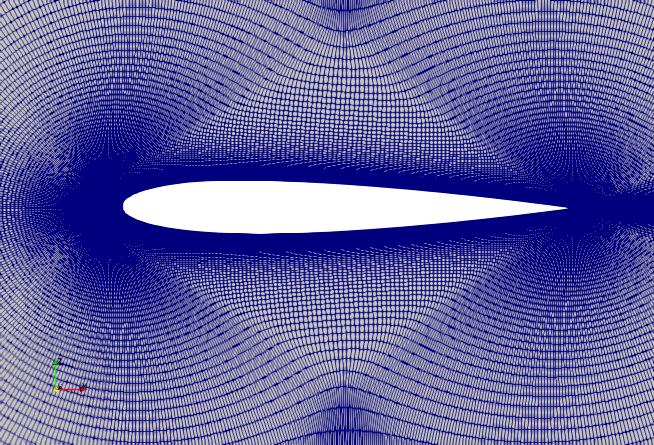
Spatial domain discretisation:
Equation discretisation:
Spatial derivatives and variables:
default: Gauss lineardiv(phi,U): bounded Gauss linearUpwind grad(U)div(phi,nuTilda): bounded Gauss linearUpwind grad(nuTilda)Gaussian linear correctedTemporal derivatives and variables:
ddtSchemes: steadyStateNumerical boundary conditions:
| Patch | Condition | Value [m⋅s-1] |
|---|---|---|
| Inlet | freestreamVelocity | \( \mathbf{U}_\alpha \) |
| Outlet | freestreamVelocity | \( \mathbf{U}_\alpha \) |
| Sides \(\text{(}y \)-dir) | empty | - |
| Aerofoil | fixedValue | (0.0, 0.0, 0.0) |
|
α | U α |
|---|---|
| \( \alpha = 0^o \) | (51.4815, 0.00, 0.0000) |
| \( \alpha = 10^o \) | (50.6994, 0.00, 8.9397) |
| \( \alpha = 15^o \) | (49.7273, 0.00, 13.3244) |
p| Patch | Condition | Value [m2⋅s-2] |
|---|---|---|
| Inlet | freestreamPressure | 0.0 |
| Outlet | freestreamPressure | 0.0 |
| Sides \(\text{(}y \)-dir) | empty | - |
| Aerofoil | zeroGradient | - |
nut (i.e. \( \nu_t \))| Patch | Condition | Value [m2⋅s-1] |
|---|---|---|
| Inlet | freestream | \( 8.58e^{-6} \approx \nu_\text{fluid} \) [82] |
| Outlet | freestream | \( 8.58e^{-6}\approx \nu_\text{fluid} \) [82] |
| Sides \(\text{(}y \)-dir) | empty | - |
| Aerofoil | fixedValue | 0.0 [82] |
nuTilda (i.e. \(\tilde{\nu}\))| Patch | Condition | Value [m2⋅s-1] |
|---|---|---|
| Inlet | freestream | \( 3.432e^{-5} \approx 4 \nu_\text{fluid} \) [82] |
| Outlet | freestream | \( 3.432e^{-5}\approx 4 \nu_\text{fluid} \) [82] |
| Sides \(\text{(}y \)-dir) | empty | - |
| Aerofoil | fixedValue | 0.0 [82] |
Solution algorithms and solvers:
| Field | Linear Solver | Smoother | Tolerance (rel) |
|---|---|---|---|
U | Smooth solvers | Gauss Seidel Smoother | 0.01 |
p | GAMG Solver | Gauss Seidel Smoother | 0.01 |
nuTilda | Smooth solvers | Gauss Seidel Smoother | 0.01 |
List of metrics:
 |  | 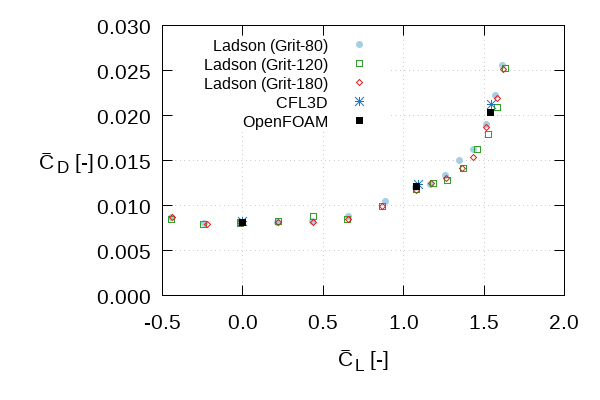 |
![Surface pressure coefficient vs. Normalised chord length at α=0 [degree]](naca0012-CP-xc-Alpha-0.png) | ![Surface pressure coefficient vs. Normalised chord length at α=10 [degree]](naca0012-CP-xc-Alpha-10.png) | ![Surface pressure coefficient vs. Normalised chord length at α=15 [degree]](naca0012-CP-xc-Alpha-15.png) |
![Surface skin friction coefficient vs. Normalised chord length at α=0 [degree]](naca0012-CF-xc-Alpha-0.png) | ![Surface skin friction coefficient vs. Normalised chord length at α=10 [degree]](naca0012-CF-xc-Alpha-10.png) | ![Surface skin friction coefficient vs. Normalised chord length at α=15 [degree]](naca0012-CF-xc-Alpha-15.png) |
Note: Links will take you to the NASA website
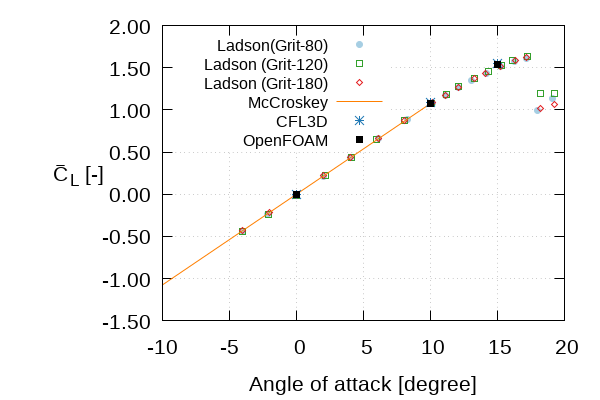
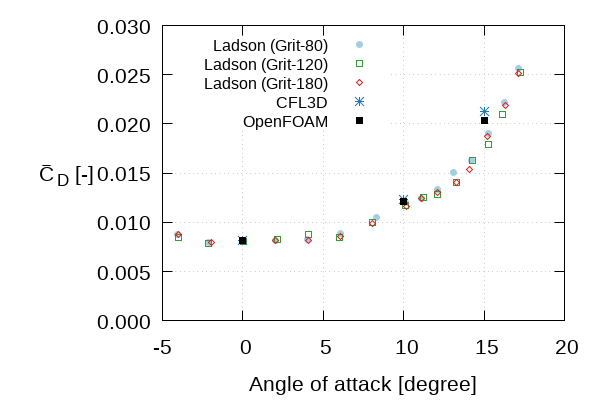
Lift and drag coefficients vs angle of attack
Pressure distribution vs local chord length
Lift coefficient vs angle of attack
Skin friction coefficient vs local chord length